Trong bài viết này mời các bạn cùng Blogsanxuat tìm hiểu về những khái niệm, công thức tính của các chỉ số trong thống kê căn bản qua ví dụ.
1. Tham số và thống kê trong thống kê căn bản
Giả sử chúng ta sẽ điều tra chiều cao của tất cả học sinh trong một trường tiểu học. Trong trường hợp này, tập dữ liệu mẹ sẽ là tất cả các trường tiểu học trên cả nước. Đặc tính chính là chiều cao. Và đặc chính này sẽ tồn tại sai lệch trong các giá trị.
Để đánh giá chiều cao của học sinh chúng ta sẽ tìm giá trị trung bình và độ lệch chuẩn của phân bố chiều cao. Độ lệch chuẩn là yếu tố thể hiện độ lớn của sai lệch.
Giả sử sau khi điều tra và tính toán được giá trị trung bình và độ lệch chuẩn, dẫu có điều tra một lần nữa chúng ta cũng không thể nhận được giá trị tương tự. Lý do bởi vì có tồn tại sai số trong dữ liệu.
Mặc dù chỉ là khái niệm, nhưng vẫn tồn tại giá trị trung bình thực và độ lệch chuẩn thực. Đây chính là những yếu tố đặc tính của tập dữ liệu mẹ mà chúng ta muốn điều tra.
Sau đây chúng ta sẽ cùng làm quen với hai khái niệm mới là Tham số và thống kê.
Tham số chính là đặc tính đại diện cho tập dữ liệu mẹ. Còn thống kê chính là đặc tính đại diện cho mẫu. Nếu xét theo ví dụ trên thì tham số chính là tất cả số học sinh tiểu học trên cả nước. Do không muốn do toàn bộ chiều cao của tất cả nên chúng ta cả đo một số lượng học sinh nhất định (thống kê) để ước tính chiều cao của học sinh tiểu học trên cả nước.
Có nghĩa là chúng ta sẽ dùng một thống kê để đánh giá một tham số. Cũng tương tự với việc chúng ta sử dụng mẫu để đánh giá tập dữ liệu mẹ.
Dưới đây là bảng các ký hiệu chúng ta thường gặp trong thống kê căn bản.
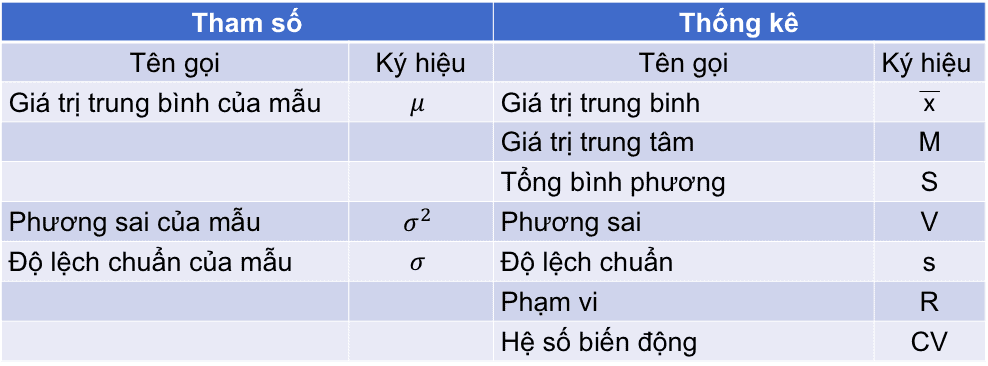
2. Thống kê biểu thị giá trị trung tâm
Chúng ta có hai thống kê biểu thị giá trị trung tâm đó là giá trị trung bình x và giá trị trung tâm M.
Giá trị trung bình
Giá trị trung bình của n dữ liệu được tính theo công thức sau. Chắc hẳn bạn cũng đã biết công thức đơn giản này rồi.
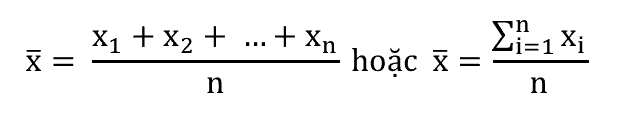
Ví dụ, nếu chúng ta có 5 dữ liệu như sau: 1, 2, 3, 4, 5. Thì giá trị trung bình sẽ là 3.
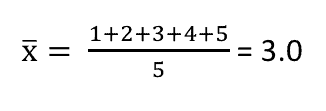
Giá trị trung tâm M
Chính là giá trị ở trung tâm khi chúng ta sắp xếp dữ liệu theo thứ tự lớn dần. Nếu số dữ liệu lẻ thì đó chính là dữ liệu ở giữa. Còn nếu số dữ liệu chẵn thì chúng ta sẽ lấy giá trị trung bình của hai dữ liệu ở giữa.
Nghe có vẻ khó hiểu nhỉ. Chúng ta sẽ cùng xem ví dụ dưới cho dễ hiểu nhé.
Trong trường hợp chúng ta có 5 dữ liệu là từ 1~5 thì giá trị trung tâm M là 3. Giá trị này không liên quan đến độ lớn nhé các bạn, chỉ xét theo thứ tự thôi.
Trong trường hợp chúng ta có 6 dữ liệu 1~6 thì giá trị trung tâm sẽ là giá trị trung bình của hai số ở giữa (3 và 4). Có nghĩa là M là 3,5.
3. Thống kê biểu thị sự sai lệch của phân bố
Chúng ta suy nghĩ ví dụ về chiều cao của học sinh tiểu học nhé.
Học sinh lớp 1 thường có chiều cao khoảng 1m. Ngược lại, học sinh lớp 5 cũng có người cao ngang người lớn. Còn học sinh lớp 3 thì chẳng có ai cao chỉ 1m nhưng cũng không có ai cao như người lớn.
Do có sự khác biệt trên nhưng nếu tính theo giá trị trung bình thì học sinh lớp 1, lớp 3 hay lớp 5 đều có chiều cao như nhau.
[su_highlight background=”#DDFF99″ color=”#000000″ class=””]Vì vậy, để đánh giá chính xác được trạng thái của tập dữ liệu mẹ thì chúng ta không chỉ dựa trên giá trị trung bình mà còn phải xem xét thêm độ lớn của sai lệch.[/su_highlight]Chúng ta sẽ cùng tính toán để tìm độ lớn sai lệch nhé.
Tổng bình phương
Tổng bình phương được tính theo công thức sau:
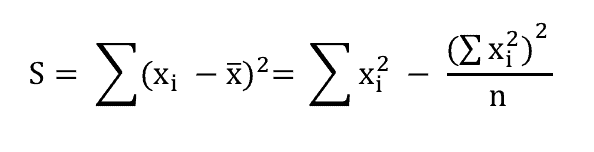
Tính tiếp theo dữ liệu bên trên chúng ta sẽ được tổng bình phương là 10
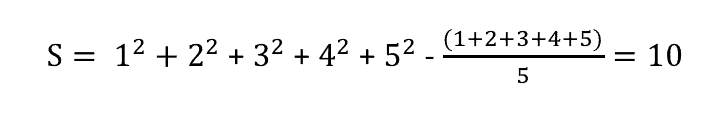
Phương sai
Tổng bình phương là một trong những thống kê thể hiện độ lớn của sai lệch. Tuy nhiên, khi số lượng dữ liệu càng lớn thì giá trị của S cũng lớn lên.
Do đó, tổng bình phương rất quan trọng trong quá trình tính độ lớn sai số nhưng không thể dùng để đánh giá trạng thái của tập dữ liệu mẹ.
Thay vào đó chúng ta sẽ sử dụng phương sai. Phương sai được tính theo công thức sau:
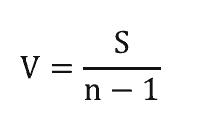
Phương sai trong ví dụ trên sẽ là 2,5.
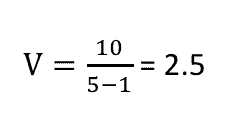
Trong đó (n-1) được định nghĩa là độ tự do của dữ liệu.
Độ lệch chuẩn
Độ lệch chuẩn là một chỉ số thống kê dùng để biểu thị độ lớn của sai lệch, được kí hiệu là s.
Độ lệch chuẩn được tính theo công thức sau:
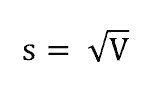
Chúng ta sẽ tính độ lệch chuẩn theo ví dụ trên và được kết quả như hình dưới.
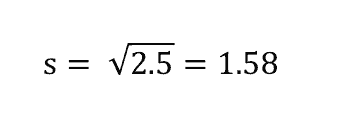
Bạn có thấy chỉ số này quen không? Thực ra, mình cũng đã nhắn đến chỉ số này trong bài biểu đồ Histogram khi đánh giá độ sai lệch của dữ liệu. Mình sẽ giới thiệu mối quan hệ này chi tiết hơn trong các bài viết tới.
[su_posts id=”112″ posts_per_page=”-1″ tax_operator=”AND” order=”desc”]
Phạm vi
Phạm vi cũng là một chỉ số dùng để đánh giá độ lớn của của sai lệch. Phạm vi được tính bằng hiệu của giá trị lớn nhất trừ đi giá trị nhỏ nhất.
R= Giá trị lớn nhất – Giá trị nhỏ nhất = x(max) – x(min)
Phạm vi tính theo ví dụ sẽ là R= 5 – 1 = 4.
Chỉ số biến động
Chỉ số biến động là chỉ số biểu thị tương đối của sai lệch.
Công thức tính chỉ số biến động:
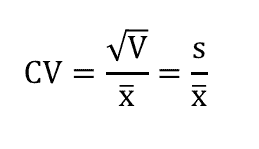
Trong một số trường hợp khi so sánh hai chi tiết có độ lớn khác nhau, đương nhiên sẽ tồn tại một khuynh hướng đương nhiên là chi tiết nhỏ sẽ có sai lệch nhỏ, chi tiết lớn sẽ có sai lệch lớn. Vì thế, để khi so sánh hai chi tiết, việc sử dụng chỉ số biến động sẽ mang lại một kết quả chính xác hơn so với việc chỉ sử dụng độ lệch chuẩn.
Như vậy, mình đã giới thiệu hết những khái niệm thống kê căn bản trong phân tích dữ liệu. Trong các bài viết tiếp theo, chúng ta sẽ cùng tìm hiểu thêm về các ứng dụng và cách áp dụng trong thực tế những kiến thức này.






dựa vào biểu đồ mà nó chỉ cho cột ngang thôi thì tính kiểu gì ạ