Gauss (1777 ~ 1855) là nhà toán học và nhà khoa học tài năng người Đức, người đã có nhiều đóng góp lớn cho các lĩnh vực khoa học, như lý thuyết số, giải tích, hình học vi phân, khoa trắc địa, từ học, thiên văn học và quang học. Ông đã phát hiện ra phân bố chính quy từ những sai lệch được hình thành trong quá trình đo vị trí của các thiên thể. Từ trong phân bố chính quy này, các mẫu thử được chọn ra và vẽ thành biểu đồ theo tần số phân bố. Biểu đồ này ngày nay được biết tới với tên gọi Histogram.

1. Histogram – Biểu đồ biểu thị sai lệch
Biểu đồ histogram là phương pháp thường được sử dụng để đánh giá sai lệch trong các công đoạn tại công xưởng. Nó được xây dựng bằng cách chia giá trị đo được thành nhiều khoảng, tập trung số dữ liệu nằm trong các khoảng đó rồi biểu thị thành biểu đồ dạng cột. Biểu đồ sau khi được hoàn thành sẽ cho chúng ta biết trạng thái của công đoạn sản xuất.
Làm nổi bật vấn đề bằng cách đánh giá sự sai lệch so với giá trị trung bình
Giả sử nếu thời gian làm việc trung bình thay đổi từ 30 phút thành 60 phút thì chúng ta sẽ biết ngay rằng ở đâu đó đã có vấn đề đã xảy ra. Tuy nhiên, cũng có những trường hợp thời gian làm việc trung bình của mỗi nhân viên trong 2 văn phòng đều là 32,1 phút nhưng do sự sai lệch khác nhau nên vẫn có thể có vấn đề trong đó.
Chúng ta sẽ cùng tìm vấn đề này bằng cách đo thử thời gian làm việc của 2 văn phòng A và B, mỗi văn phòng có 20 nhân viên. Kết quả đo được sẽ được phân chia theo khoảng cách nhau 5 phút và biểu thị thành biểu đồ. Nhìn vào kết quả đo được, chúng ta sẽ thấy ngay người làm nhanh nhất tại văn phòng A chỉ hết 22 phút, trong khi người làm chậm nhất sẽ tiêu tốn 44 phút. Tương tự như thế đối với văn phòng B, người làm nhanh nhất thậm chí chỉ hết 17 phút nhưng lại có người làm tới 48 phút.
Nếu bạn muốn đánh giá trạng thái làm việc của 2 văn phòng này bằng thị giác thì biểu đồ Histogam là một công cụ hữu hiệu. Ngoài ra, trên biểu đồ này còn biểu thị giá trị trung bình và độ lệch tiêu chuẩn. Ở cả 2 văn phòng này đều có thời gian làm việc trung bình là 32,1 phút nhưng độ lệch tiêu chuẩn tại văn phòng A là 5,86 và của B là 7,71. Chúng ta có thể thấy độ lệch tiêu chuẩn của B gấp tới 1,3 lần của A nên có thể kết luận rằng tại văn phòng B đang có vấn đề gì đó.

2. Xây dựng bảng tần số
Bảng tần số rất quan trọng và có thể nói rằng đây chính là nên tảng trong quá trình lập biểu đồ Histogram. Bảng tần số sẽ được xây dựng theo các bước sau dựa trên dữ liệu đã thu thập về chiều cao của 60 người.

– Bước 1: Thu thập dữ liệu Số dữ liệu n = 60
– Bước 2: Tìm giá trị nhỏ nhất và lớn nhất Giá trị lớn nhất x-max = 186 cm, giá trị nhỏ nhất x-min = 160 cm
– Bước 3: Quyết định số khoảng chia Khoảng chia được tính bằng cách lấy căn bậc 2 của số biến số (số người đã đo chiều cao) √n = √60 = 7,75 → 8 (số khoảng chia)
– Bước 4: Quyết định độ rộng của mỗi khoảng chia Độ rộng khoảng chia = (Giá trị lớn nhất – giá trị nhỏ nhất)/ số khoảng chia = (186 – 160)/8 = 3,25 Thực tế, độ rộng khoảng chia được tính theo tích đơn vị đo nhỏ nhất với một số nguyên. Do đơn vị đo nhỏ nhất ở đây là 1 cm nên chúng ta chọn độ rộng khoảng chia là 3.
– Bước 5: Quyết định ranh giới trên dưới của khoảng chia Ranh giới của một khoảng chia được tính như sau: Ranh giới dưới = giá trị nhỏ nhất – ½ đơn vị đo nhỏ nhất Đối với khoảng 1: Ranh giới dưới = 160 – ½ x 1 = 159,5 Ranh giới trên = Ranh giới dưới + Độ rộng khoảng chia Đối với khoảng 1 : Ranh giới trên = 159,5 + 3 = 162,5 Giá trị trung tâm = (Ranh giới trên + Ranh giới dưới)/2 Đối với khoảng 1: (159,5+162,5)/2 = 161 Tương tự như vậy chúng ta có thể tính được ranh giới của tất cả các khoảng như bảng dưới.
– Bước 6: Tổng hợp các khoảng để tạo thành bảng tần suất 3. Vẽ biểu đồ Histogram Sau khi kết thúc 6 bước ở phần trước chúng ta đã có một bảng tần xuất hoàn chỉnh với đầy đủ các số liệu. Những số liệu này sẽ được sử dụng để xây dựng biểu đồ Histogram.

– Bước 7: Quyết định tỷ lệ Trục hoành sẽ biểu thị giá trị trung tâm của các khoảng và trục tung sẽ biểu thị tần số của từng dữ liệu.
– Bước 8: vẽ biểu đồ dạng cột Vẽ các cột dựa vào giá trị trung tâm cho từng khoảng. Chú ý chúng ta sẽ không để khoảng trống giữa các cột.
– Bước 9: Điền giá trị trung bình Sau khi tính giá trị trung bình, hãy biểu thị giá trị này bằng đường nét đứt trên biểu đồ.
Bước 10: Điền các mục còn lại vào biểu đồ Những thông tin quan trọng khác của biểu đồ như số dữ liệu, giá trị trung bình, sai lệch tiêu chuẩn.
Những điều có thể hiểu được từ biểu đồ Histogram Khi nhìn vào biểu đồ chúng ta có thể thấy được một số điều như sau: – Giá trị trung tâm của phân bố nằm ở đâu? – Độ không đồng đều của dữ liệu lớn hay nhỏ? – Dữ liệu phân bố theo dạng nào ? (tham khảo phần 4) – So sánh với giá trị tiêu chuẩn đề đánh giá năng lực của công đoạn
4. Cách nhìn biểu đồ Histogram
Sau khi tác thành biểu đồ Histogram, chúng ta chỉ thoáng nhìn là có thể hiểu được trạng thái phân bố của dữ liệu. Hình dạng của biểu đồ sẽ giúp chúng ta nắm bắt được vấn đề cần giải quyết.
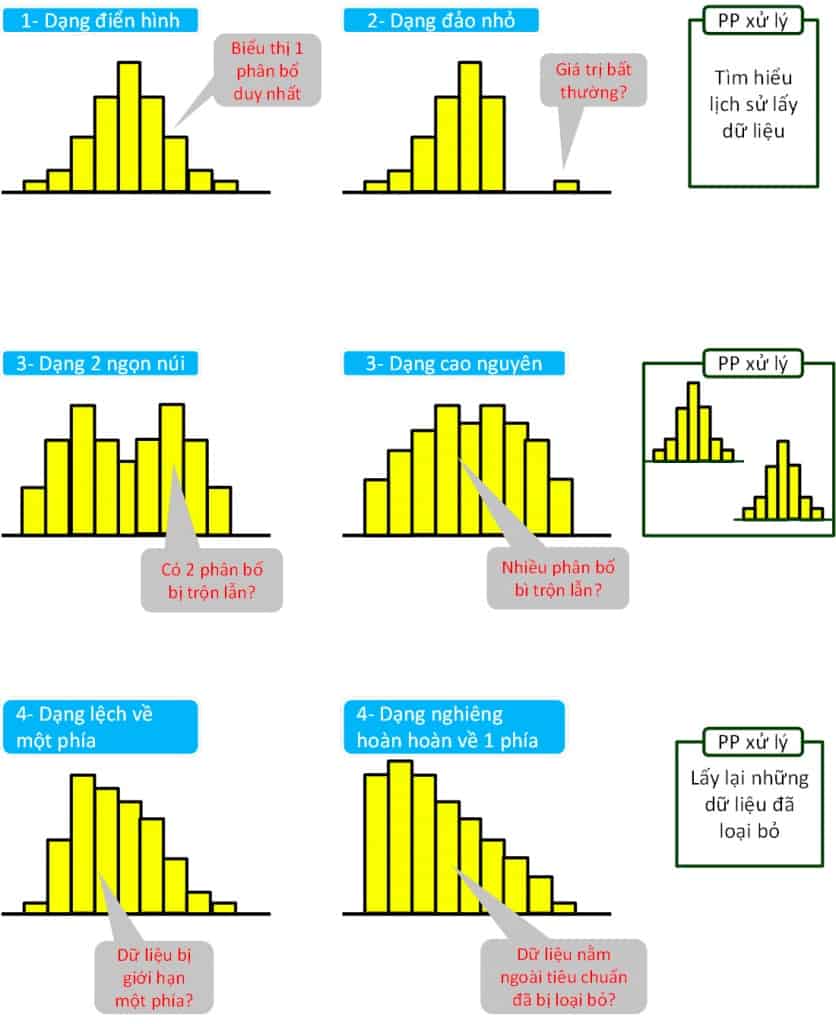
• Dạng chung: Tần số sẽ lớn dần khi tiến gần về phía trung tâm và nhỏ dần khi dịch chuyển về 2 phía. Khi công đoạn trong trạng thái ổn định thì dữ liệu sẽ có dạng này.
• Dạng có đảo nhỏ tách riêng: Ở dạng này sẽ xuất hiện dữ liệu nằm tách riêng về một phía so với các dữ liệu còn lại. Dạng này thường gặp khi có một phần dữ liệu bất thường được trộn lẫn vào. Nếu đây là dữ liệu do sai sót khi đo đạc thì chúng ta có thể bỏ đi. Nhưng nếu đây không phải dữ liệu do sai sót thì nên xem lại quá trình đo dữ liệu này để tìm vấn đề.
• Dạng 2 ngọn núi hay cao nguyên: Với dạng 2 ngọn núi thì càng gần trung tâm tần số sẽ càng giảm và hình thành 2 ngọn núi ở hai bên. Dạng này được hình thành có thể do sự trộn lẫn của 2 loại dữ liệu có phân bố khác nhau. Với dạng cao nguyên, tần số giữa các khoảng hầu như không thay đổi nhiều. Đây có thể thì phân bố đã bị lẫn nhiều loại dữ liệu khác nhau. Trong trường hợp này, hãy thử phân tầng thành 2 hay nhiều phân bố có giá trị trung bình khác nhau rồi vẽ riêng thành từng biểu đồ. Sau đó, xem xét vấn đề.
• Dạng lệch về một phía hay lệch hoàn toàn về một phía: Dạng lệch về một phía, giá trị trung bình sẽ không nằm ở giữa mà thiên về một trong 2 phía, biểu đồ có dạng bất đối xứng. Với dạng biểu đồ này chúng ta có thể phán đoán rằng dữ liệu đã bị giới hạn một phía (phía không bình thường) bởi một tiêu chuẩn nào đó. Còn dạng lệch hoàn toàn thì dữ liệu sẽ dồn hoàn toàn về một phía giống như một bức tường. Dạng này thường xuất hiện khi các dữ liệu nằm ngoài tiêu chuẩn đã bị loại bỏ. Đối với cả 2 trường hợp trên, chúng ta nên đưa cả những dữ liệu bị giới hạn hay bị loại bỏ bởi tiêu chuẩn vào để xem xét và tìm vấn đề.
5. So sánh kết quả với tiêu chuẩn
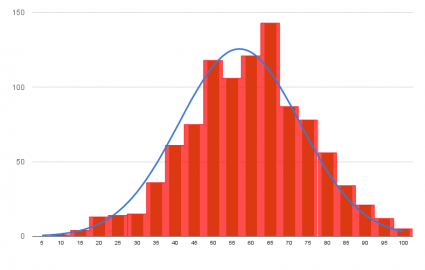
So sánh khoảng rộng của dữ liệu với khoảng rộng tiêu chuẩn Việc so sánh biểu đồ histogram với giá trị tiêu chuẩn sẽ cho chúng ta biết được năng lực của công đoạn có thỏa mãn những yêu cầu kĩ thuật hay không. Cụ thể, nếu điền giá trị tiêu chuẩn hoặc giá trị mục tiêu lên biểu đồ Histogram, chúng ta sẽ thấy ngay giá trị trung bình sai lệch bao nhiêu so với tiêu chuẩn hay mục tiêu, hay dữ liệu có nằm trong khoảng tiêu chuẩn hay không. Từ kết quả nhận được, chúng ta có thể dễ dàng nắm bắt được vấn đề (nếu có) của công đoạn sản xuất ở trạng thái hiện tại.

– Trường hợp lí tưởng: sai lệch của sản phẩm hay công việc đều nằm trong tiêu chuẩn, và giá trị trung bình cũng đồng nhất với giá trị trung tâm của tiêu chuẩn. Đây là trạng thái lý tưởng và cần duy trì.
– Trường hợp không có dư thừa ở một phía: Sai lệch của sản phẩm hay công việc đều tập trung bên trong khoảng tiêu chuẩn nhưng giá trị trung bình lại bị lệch sang một phía. Ở trạng thái này, nếu thì cần có thay đổi nhỏ trong công đoạn sản xuất cũng có thể đưa sai lệch ra khỏi khoảng tiêu chuẩn. Trong những trường hợp như thế này thì phương án khắc phục tốt nhất là thực hiện cách đối sách để giảm giá trị trung bình và giảm sai lệch.
– Trường hợp không có dư thừa ở cả hai phía: Sai lệch của sản phẩm hay công việc vừa đủ nằm trong khoảng tiêu chuẩn. Đây không phải là trạng thái mà chúng ta có thể an tâm, có thể dự đoán được việc dữ liệu sẽ lệch khỏi tiêu chuẩn bất cứ lúc nào. Trong trường hợp này, việc đưa ra các phương án xử lý nhằm thu nhỏ sai lệch để tạo thêm khoảng dư thừa ở hai phía là rất quan trọng.



Độ sai lệch dữ liệu tính như thế nào bạn nhỉ?
Bạn có tham khảo cách tính độ sai lệch dữ liệu trong bài viết dưới đây nhé.
http://blogsanxuat.com/phan-tich-du-lieu-thong-ke-can-ban-va-bieu-do/
tính mean và sd kiểu gì vậy?, mình có tham khảo link bên trên rồi nhưng không có áp dụng cho đồ thị được.
bạn có thể tính mean = hàm average trong excel và sd = hàm stdv trong excel, hoặc có thể dùng mô tả thống kê, bạn vào data/data analysis/descripiton statistic/ chọn các thông số để nó ra bảng thống kê mô tả cho bảng dữ liệu đó
còn bằng thủ công bạn tính mean = trung bình cộng của các số lại còn tính Stdv = căn bậc 2 của tổng bình phương ví dụ
có dãy số : 1, 2, 3, 4, 5, 6
=tính mean =1+2+3+4+5+6 = 21/6=3.5 hoặc công thức average trong excel nhé
tính độ lệch chuẩn = https://huannghe.edu.vn/cong-thuc-tinh-do-lech-chuan/ bạn nhé
Nếu biểu đồ phân số có 2 đỉnh bằng nhau, thiết bị máy móc đang gặp vấn đề phải không bạn?
Biểu đồ phân bố ạ